Chain Dimensions
Entanglement & Crossover Length

It is well-known that the viscoelastic properties of many linear polymers vary with molecular weight in basically the same manner. For example, the melt viscosity of short polymer chains (η) is linear proportional to the molecular weight M (or, more precisely, its weight-average, since most polymer samples are not perfectly monodisperse), whereas that of long polymer chains shows a much stronger molecular weight dependence. The smooth crossover between these two regimes occurs at the critical molecular weight M_c whose value is characteristic of a polymer.

η₀  = K · M,  M < M_c

η₀  = K · M^3.4,  M > M_c

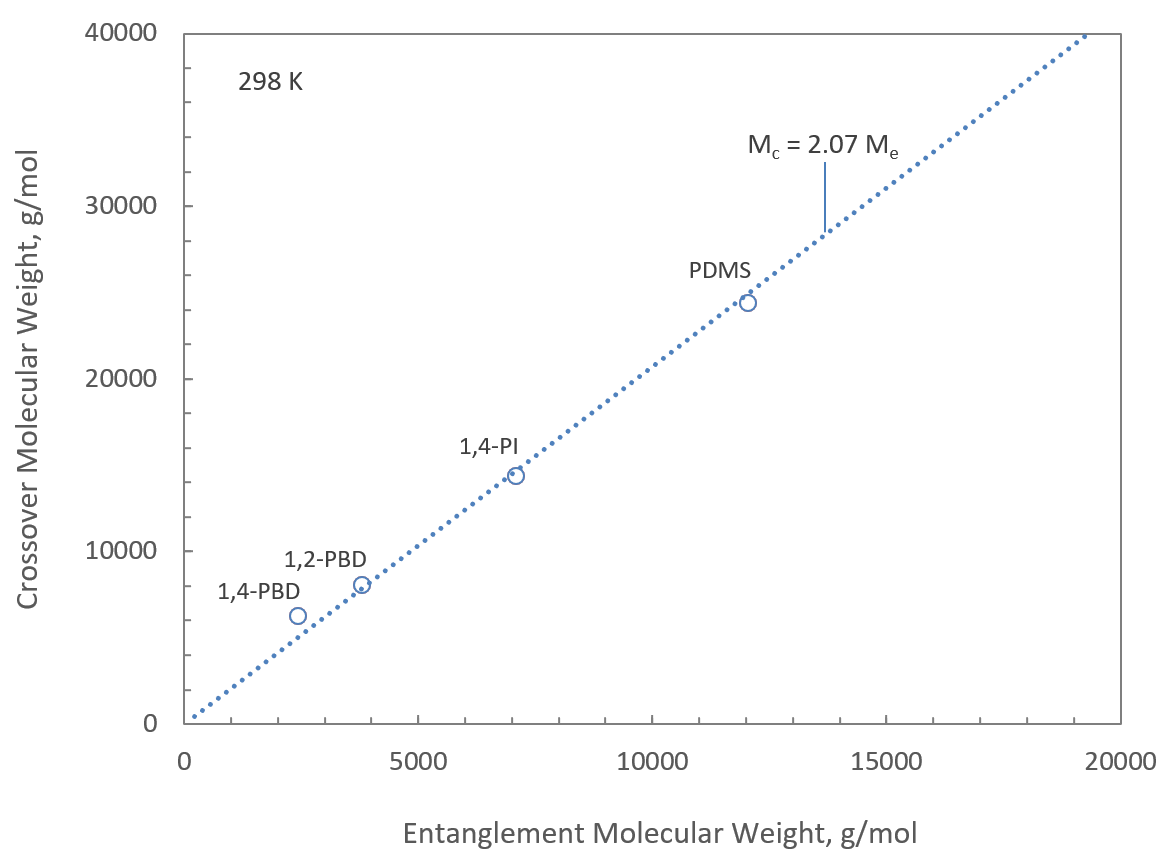
The much stronger dependence of rheology on structure above the critical molecular weight M_c has been explained by entanglement interactions. When each polymer chain is entangled with at least two other chains, the polymers form a three-dimensional network of entanglements.¹ Thus, the crossover between the two regimes occurs at about two times the entanglement weight, M_c ≈ 2M_e. The parameter M_e, is typically calculated from the plateau storage modulus (G_N,0) of the polymer in its melt or rubbery state:²

G_p = 4/5 · ρ R T / M_e

where R is the universal gas constant (R = 8.314 K^-1), T is the temperature, and ρ is the polymer melt density. The relationship M_c ≈ 2M_e holds for many linear polymers with a glass transition temperature well below room temperature (see figure below).

 

However, as Fetter, Lohse, and Milner have shown,³ the crossover molecular weight M_c of many other linear polymers can be noticeably larger or smaller than 2M_e, or in other words, the long-held notion that the ratio M_c / 2M_e equals about unity for all linear polymers is incorrect. This finding is surprising because of the generally good agreement of many properties in the theta- and melt-state. Krishnamoorti, Graessley et al.⁴ postulated that most differences in the melt and theta state behavior can be explained by conformational changes induced by solvent molecules, that is, the population of gauche and trans states in solution can differ from that in the melt state depending on the solvent used.

Polymer chain dimensions in a theta-solvent are often evaluated via intrinsic viscosity measurements, as follows:⁶

K_θ = [η]_θ  / M^1/2 = Φ_θ ⟨R_h,0²⟩ / M^3/2

where K_θ is the Mark-Houwink parameter and R_h,0 the hydrodynamic radius of an unperturbed polymer.

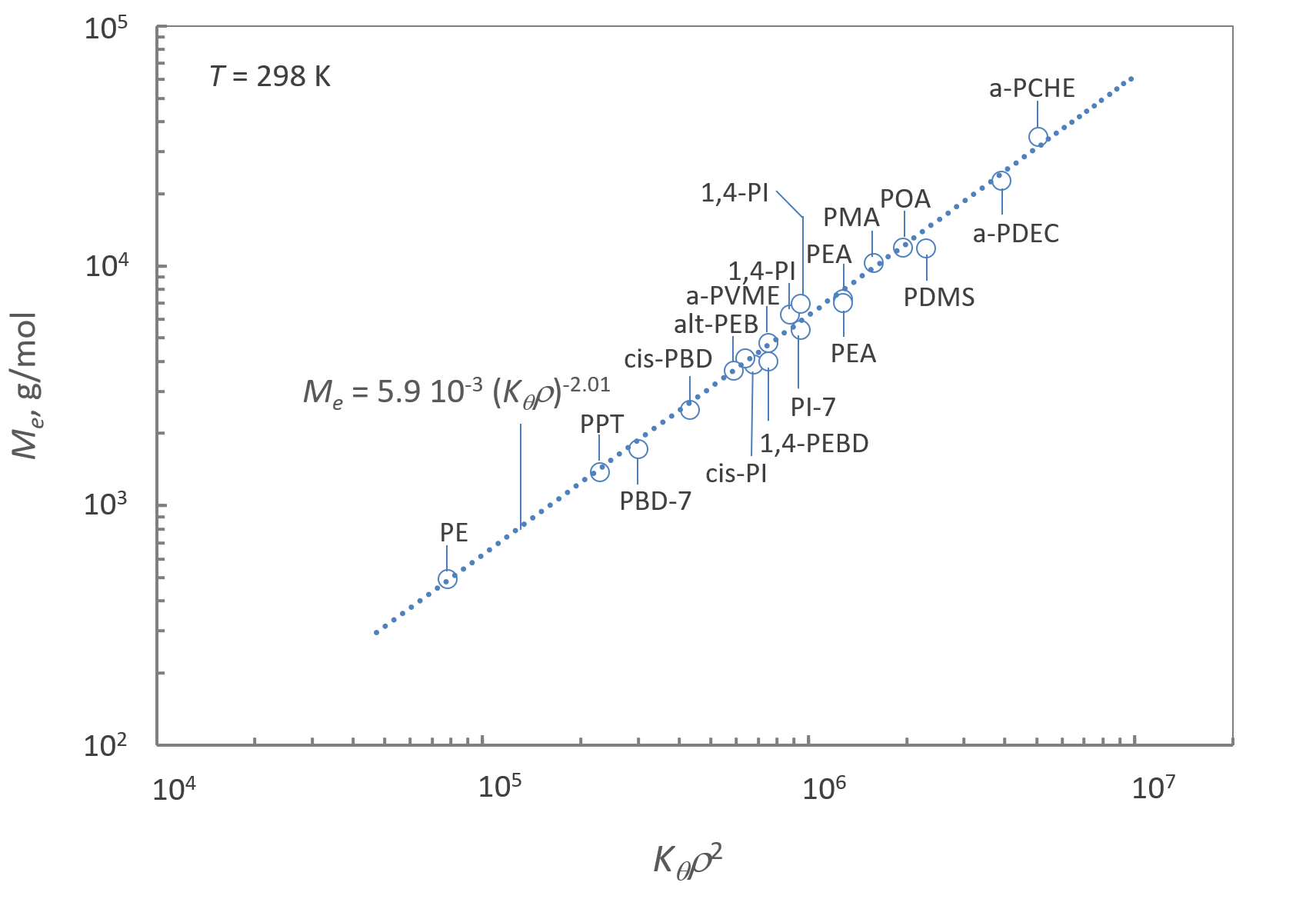
As has been shown by Fetters et al.⁵, the entanglement weight M_e can be calculated from the Mark-Houwink parameter K_θ = [η]_θ  / M^1/2 and the amorphous polymer density ρ:

M_e = [Φ_θn_t / N_aρK_θ]²

where N_a denotes the Avogadro number, and n_t the number of entanglement strands in a volume with dimensions equal to the diameter of the corresponding reptation tube. Thus, a plot of M_e against (ρK_θ)^-2 should yield a straight line, as it is the case for a large number of polymers (see Figure below).

 

This result is further proof that the conformational properties of polymers in solution and melt are related to their viscoelastic properties. Therefore, measurements of the molecular dimensions such as size exclusion chromatography, light and small angle neutron scattering, can be utilized to predict the viscoelastic properties of many polymers.

References and Notes

1. A good analogy is a bowl of spaghetti. When the individual strands of spaghetti are short, they can be easily separated, whereas long strands are very difficult to separate from one the other due to the entanglements.

2. M. Doi & S. F. Edwards, The Theory of Polymer Dynamics, Oxford Univ. Press, New York 1986
3. Lewis J. Fetters, David J. Lohse, and Scott T. Milner, Macromolecules, 32, 6847-6851 (1999)
4. R. Krishnamoorti et al., J. Poly. Sci.: Part B: Poly. Phys., 40, 1768–1776 (2002)
5. L.J. Fetters, D.J. Lohse, D. Richter, T.A. Witten, A. Zirkel, Macromolecules, 27, 4639 (1994)